Biomathematics: Where Mathematics Meets Complexity of Life

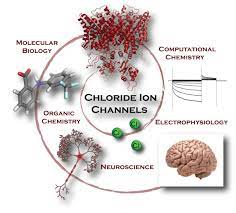
Biomathematics, also known as mathematical biology, is a unique and interdisciplinary field that applies mathematical principles and techniques to study and understand biological systems. This field serves as a bridge between mathematics and biology, enabling scientists to model, analyze, and make predictions about a wide range of biological phenomena. In this article, we will explore the world of biomathematics, uncover its key concepts, applications, and the crucial role it plays in unraveling the complexity of life.

The Essence of Biomathematics

Biomathematics focuses on using mathematical tools and modeling to gain insights into various biological processes and systems. It encompasses a wide array of subfields, including:

1. Population Dynamics: Population biomathematics deals with the study of how populations of species change over time, taking into account factors like birth rates, death rates, and migration.
2. Epidemiology: Epidemiologists use mathematical models to understand and predict the spread of diseases within populations.
3. Ecological Modeling: Biomathematics plays a crucial role in modeling ecological interactions, species distribution, and ecosystem dynamics.
4. Pharmacokinetics: In pharmacology, biomathematics aids in understanding how drugs are absorbed, distributed, metabolized, and excreted by the body.
5. Neuroinformatics: Neurobiologists use mathematical models to simulate and understand the complex processes that occur in the nervous system.
6. Genomic Analysis: Biomathematics contributes to the analysis of genetic data, including gene expression, DNA sequencing, and evolutionary genomics.

The Principles of Biomathematics

Biomathematics is guided by several fundamental principles:

1. Mathematical Modeling: Biomathematicians construct mathematical models that describe real-world biological phenomena. These models can be based on differential equations, probability theory, and other mathematical frameworks.
2. Data Analysis: Biomathematics involves the analysis of biological data, using statistical methods to draw meaningful conclusions and make predictions.
3. Interdisciplinary Collaboration: Collaboration between biologists and mathematicians is essential to translate biological questions into mathematical problems and vice versa.
4. Predictive Power: Biomathematical models provide predictive power, allowing researchers to anticipate the behavior of biological systems under various conditions.
5. Feedback Loops: Models are refined based on experimental data, creating a feedback loop that leads to more accurate and realistic representations of biological systems.

Applications of Biomathematics

Biomathematics has a broad range of practical applications, including:

• Epidemiological Forecasting: Biomathematical models are used to predict the spread of infectious diseases, helping public health officials make informed decisions.
• Conservation Biology: Biomathematics aids in the design of conservation strategies for endangered species and the management of natural resources.
• Pharmaceutical Development: The field contributes to drug development by modeling drug interactions and pharmacokinetics.
• Precision Medicine: Biomathematics is integral to the concept of precision medicine, where treatment is tailored to an individual’s unique genetic makeup.
• Agriculture: Biomathematics is applied in crop modeling, optimizing planting and harvesting schedules, and pest control.
• Ecological Management: It aids in the management of ecosystems and understanding the impact of climate change on biodiversity.

Biomathematical Techniques

Biomathematicians employ a variety of techniques to study and model biological systems:

1. Differential Equations: These equations are commonly used to model changes in populations, biochemical reactions, and many other biological processes.
2. Agent-Based Modeling: In agent-based modeling, individual entities (agents) are simulated, each following a set of rules. This is useful for simulating complex interactions in ecology and social sciences.
3. Statistical Analysis: Biomathematics extensively uses statistical methods to analyze experimental data and make inferences.
4. Genomic Sequencing and Analysis: Biomathematicians use mathematical approaches to analyze large-scale genomic data and identify genetic patterns.
5. Network Theory: Network theory is used to study complex biological systems, such as protein-protein interaction networks or ecological food webs.

Notable Discoveries

Biomathematics has contributed to several notable discoveries and advancements in science:

• Epidemiology: Mathematical models have played a pivotal role in understanding the dynamics of infectious disease outbreaks, such as the modeling of COVID-19 transmission.
• Population Dynamics: Biomathematical models have helped predict and manage the populations of endangered species and understand invasive species’ impact on ecosystems.
• Pharmacokinetics: Biomathematics aids in optimizing drug dosages and predicting drug interactions, leading to safer and more effective medications.
• Genomics: The field has advanced our understanding of genetic variation, gene expression, and the mechanisms underlying diseases.
• Neuroinformatics: Mathematical models of neural networks have provided insights into brain function and disorders.

Future Challenges and Opportunities

Biomathematics faces ongoing challenges and opportunities:

• Complexity: As biological data becomes more complex, biomathematicians must develop advanced models and computational tools to handle this complexity.
• Interdisciplinary Training: There is a growing need for scientists with expertise in both biology and mathematics to foster collaboration and tackle complex biological questions.
• Personalized Medicine: Biomathematics will continue to play a significant role in the development of personalized medical treatments.
• Environmental Conservation: As climate change and habitat loss threaten biodiversity, biomathematics will be crucial in developing effective conservation strategies.

Conclusion

Biomathematics serves as a powerful tool for understanding the intricate processes of life through mathematical modeling and data analysis. By leveraging mathematical principles, biomathematics contributes to advancements in medicine, ecology, epidemiology, and genetics.

As our understanding of biology deepens and technology evolves, biomathematics will remain at the forefront of interdisciplinary research, addressing complex biological questions and contributing to the well-being of both human populations and the natural world.